Chapter 6 Manifold Learning
6.1 The Manifold Hypothesis
In Chapter 4, we focused our attention on linear manifolds and saw cases where this structure was insufficient. Using kernel PCA, we tried to find a workaround by first (implicity) mapping our data to a higher dimensional feature space then approximating results with linear subspaces (of feature space). In this Chapter, we will investigate several methods to estimate a lower-dimensional representation assuming the data live on a manifold, which we hereafter refer to as the manifold hypothesis. This hypothesis is the central assumptions of modern nonlinear dimension reduction methods and can be stated as follows.
Definition 6.1 (Manifold Hypothesis) The observed data \(\vec{x}_1,\dots,\vec{x}_N\in\mathbb{R}\) are concentrated on or near a manifold of intrinsic dimension \(t\ll d.\)
In the following sections, we will provide more background on the mathematical foundation of nonlinear manifolds. Specifically, what is a manifold (and what is not) and what do we mean by intrinsic dimensionality. We’ll also touch on important properties which guides the assumptions used by various methods of nonlinear dimension reduction. For now, let’s discuss a simple mechanism for generating data on a manifold.
Assume there are points \(\vec{z}_1,\dots,\vec{z}_N\in A \subset \mathbb{R}^t\) which are iid random samples from some probability distribution. These points are (nonlinearly) mapped into a higher dimensional space \(\mathbb{R}^d\) by a smooth map \(\Psi\) giving data \(\vec{x}_i = \Psi(\vec{z}_i)\) for \(i=1,\dots,N.\) Hereafter, we refer to \(\Psi\) as the manifold map. In this setting, we are only given \(\vec{x}_1,\dots,\vec{x}_N\), and we want to recover the lower-dimensional \(\vec{z}_1,\dots,\vec{z}_N\). If possible, we would also like recover \(\Psi\) and \(\Psi^{-1}\) and in the most ideal case, the sampling distribution that generated the lower-dimensional coordinates \(\vec{z}_1,\dots,\vec{z}_N\).
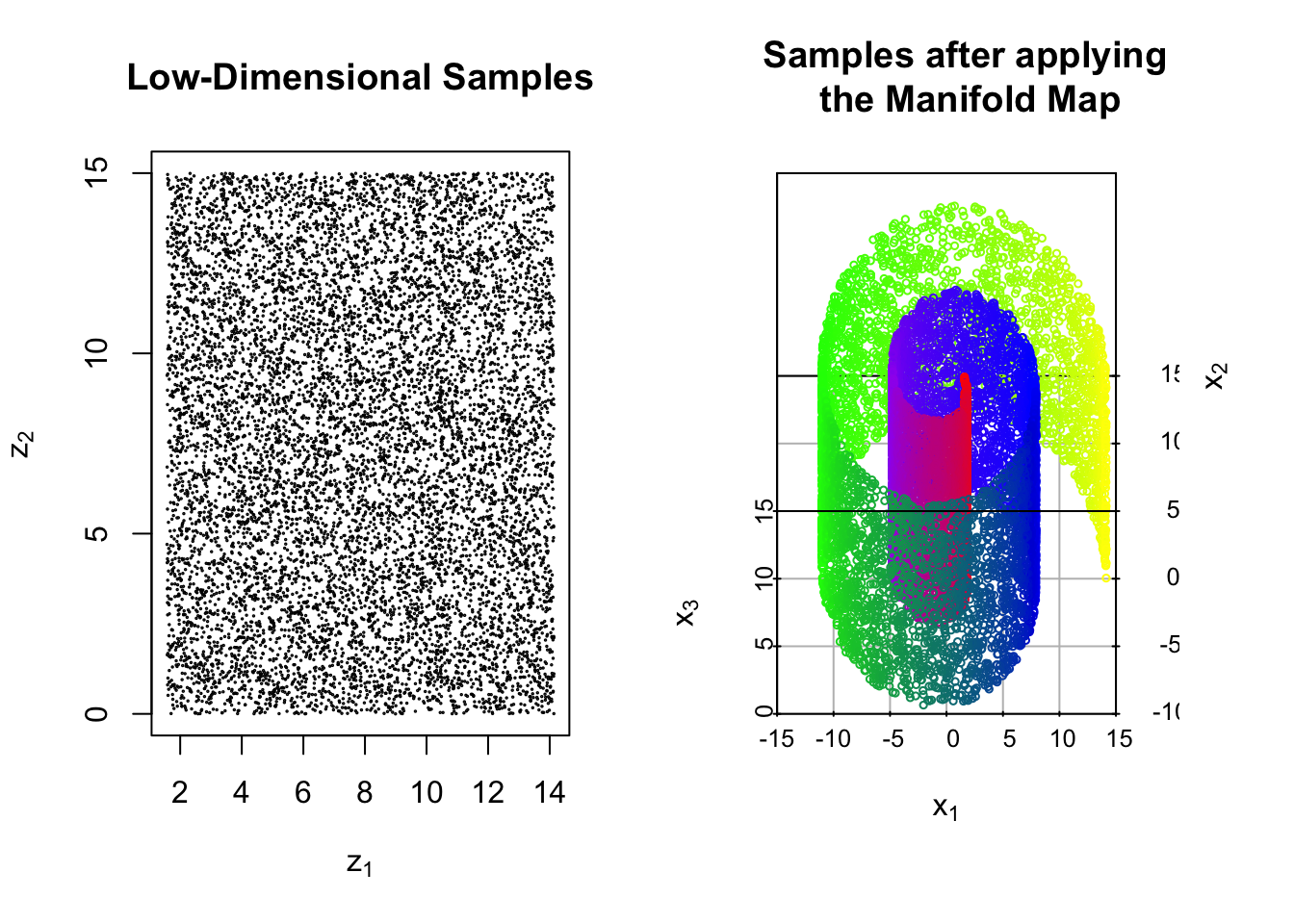
Example 6.1 (Mapping to the Swiss Roll) Let \(A = (\pi/2,9\pi/2)\times (0,15)\). We define the map \(\Psi:A\to \mathbb{R}^3\) as follows
\[\Psi(\vec{z}) = \Psi(z_1,z_2) = \begin{bmatrix} z_1\sin(z_1) \\ z_1\cos(z_1) \\ z_2 \end{bmatrix}\]
Below we show \(N=10^4\) samples which are drawn uniformly from \(A\). We then show the resulting observations after applying map \(\Psi\) to each sample.
We may also consider the more complicated case where the observations are corrupted by additive noise. In this setting, the typical assumption is that the noise follows after the manifold map so that our data are \[\vec{x}_i = \Psi(\vec{z}_i) + \vec{\epsilon}_i, \qquad i = 1,\dots, N\] for some noise vectors \(\{\vec{\epsilon}_i\}_{i=1,\dots,N}.\)
Example 6.2 (Swiss Roll with Additive Gaussian Noise) Here, we perturb the observations in the preceding example with additive \(\mathcal{N}(\vec{0},0.1{\bf I})\) noise.
In addition to the goals in the noiseless case, we may also add the goal of learning the noiseless version of the data which reside on a manifold.
However, there are a number of practical issues to this setup. First, the dimension, \(t\), of the original lower-dimensional points is typically unknown. Similar to previous methods, we could pick a value of \(t\) with the goal of visualization, base our choice off of prior knowledge, or run our algorithms different choices of \(t\) and compare the results. More advanced methods for estimating the true value of \(t\) are an open area of research [20].
There is also a issue with the uniqueness problem statement. Given only the high dimensional observations, there is no way we could identify the original lower-dimensional points without more information. In fact, one could find an unlimited sources of equally suitable results.
Let \(\Phi:\mathbb{R}^t\to\mathbb{R}^t\) be an invertible function. As an example, you could think of \(\Phi\) as defining a translation, reflection, rotation, or some composition of these operations akin to the nonuniqueness issue we addressed in classical scaling. If our original observed data are \(\vec{x}_i = \Psi(\vec{z}_i)\), our manifold learning algorithm could instead infer that the manifold map is \(\Psi \circ \Phi^{-1}\) and the lower-dimensional points are \(\Phi(\vec{z}_i)\). This is a perfectly reasonable result since \((\Psi\circ \Phi^{-1})\circ\Phi(\vec{z}_i) = \Psi(\vec{z}_i)= \vec{x}_i\) for \(i=1,\dots,N\), which is the only result we require. Without additional information, there is little we could do to address this issue. For the purposes of visualization, however, we will typically be most interested in the relationship between the lower-dimensional points rather than their specific location or orientation. As such, we need not be concerned about a manifold learning algorithm that provides a translated or rotated representation of \(\vec{z}_1,\dots,\vec{z}_N.\) More complicated transformations of the lower-dimensional coordinates are of greater concern and may be addressed through additional assumptions about the manifold map \(\Psi.\)
In the following sections, we will review a small collection of different methods which address the manifold learning problem. Many of the methods are motivated based on important concepts from differential geometry, the branch of mathematics focused on manifolds. Many of the details of differential geometry are beyond the scope of this book, so we will focus on a few key ideas here. For the more mathematically-minded reader, see [21, 22].
6.2 Brief primer on manifolds
While our data may exhibit some low-dimensional structure, there is no practical reason to expect such behavior to be inherently linear. In the resulting sections, we will explore methods which consider nonlinear structure and assume the data reside on or near a manifold. Such methods are referred to as nonlinear dimension reduction or manifold learning. Critical to this discussion is the notion of a manifold.
Definition 6.2 (Informal Definition of a Manifold) A manifold is a (topological) space which locally resembles Euclidean space. Each point on a \(t\)-dimensional manifold has a neighborhood that can be mapped continuously to \(\mathbb{R}^t\). We call \(t\) the intrinsic dimension of the manifold.
We’ll return to mathematical details shortly, but let’s stick with intuition for now. If you were to stand at any point on a \(k\)-dimensional manifold, the portion of the manifold closest to you look just like a \(k\)-dimensional hyperplane – though you might need to be extremely near-sighted for this to be true. The canonical example is the surface of the Earth. If we take all points on the surface of the Earth, they form a sphere in \(\mathbb{R}^3\). However, if we focus on the area around any point it looks like a portion of the two-dimensional plane. In fact, we can represent any point on the surface of the Earth in terms of two numbers, latitude and longitude. In the language of manifolds, we can say the surface of the Earth is a manifold with intrinsic dimension two which has been embedded in \(\mathbb{R}^3\). Here are a few more concrete examples.
Example 6.3 (Examples of Manifolds) Many familiar geometric objects are manifolds such as lines, planes, and spheres. For example, Let \(\vec{w}_1,\dots,\vec{w}_k\in\mathbb{R}^d\) be a set of linearly independent vectors. Then \(\text{span}(\vec{w}_1,\dots,\vec{w}_k)\) is a \(k\)-dimensional manifold in \(\mathbb{R}^d.\) When \(k=1\), the span is a line; for \(k>1\) the span is a hyperplane. The sphere unit sphere \(\{\vec{x}\in\mathbb{R}^d:\,\|\vec{x}\|=1\}\) is a \(d-1\) dimensional manifold. For example, when \(d=3\) manifold resembles the surface of the earth which locally looks like a portion of the 2-dimensional plane. The swiss roll example above is a two-dimensional manifold in \(\mathbb{R}^3\).
In short manifold as a nice smooth, curved surface. There are several reasons why a subset may not be a manifold. The most straightforward examples are cases where the manifold as a self intersection or a sharp point.
Example 6.4 (Non-manifold) Consider a figure eight curve. At the midpoint where the upper and lower circle meet, there is not neighborhood that resembles Euclidean space so the surface is not a manifold.
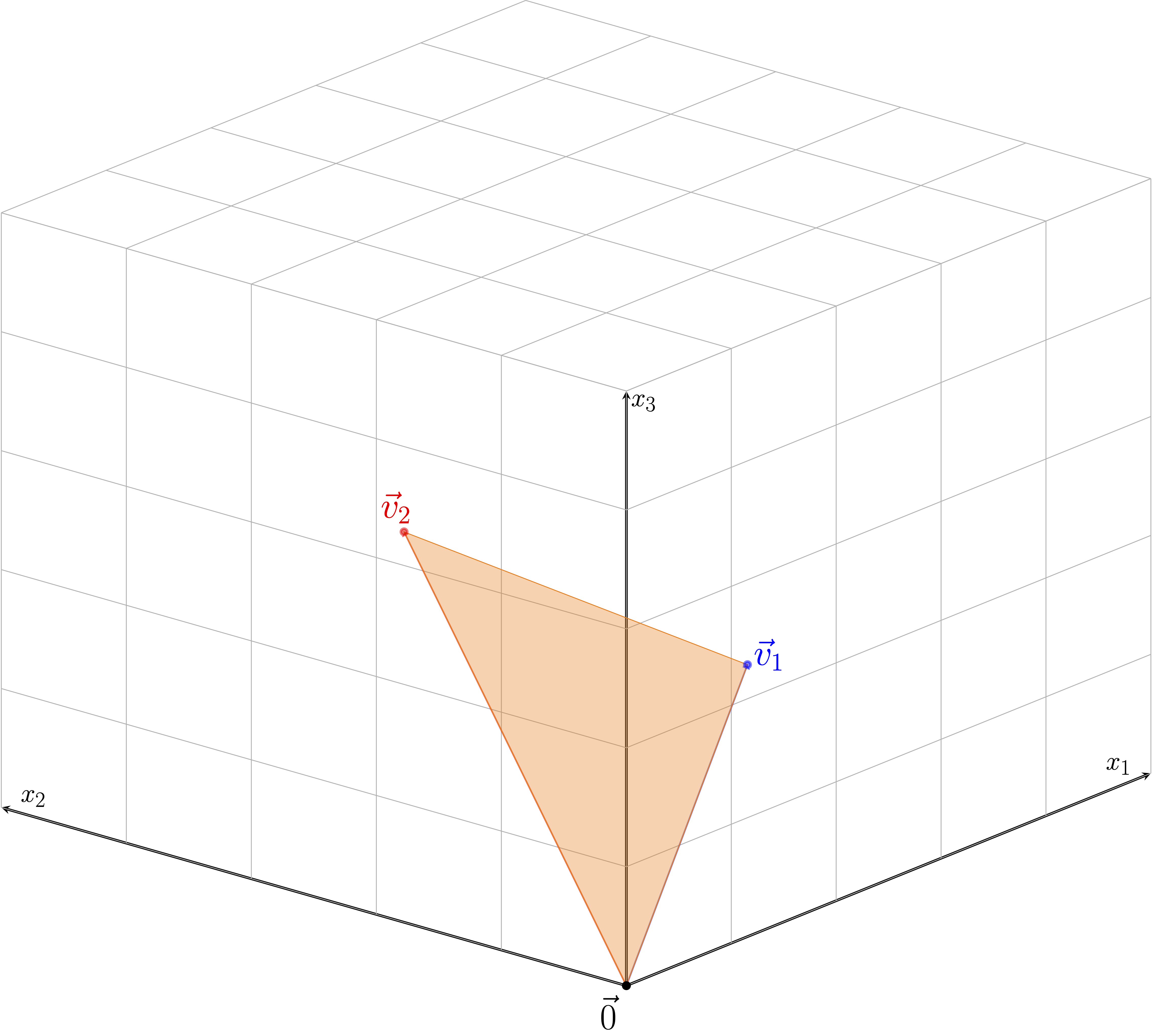
For a second example, take any two vectors \(\vec{h}_1\) and \(\vec{h}_2\) and consider there convex hull, that is \(\{a\vec{h}_1+b\vec{h}_2: a,b > 0, a+b\le 1\}\) such the orange triangle in the figure below. At the three vertices of the orange triangle, there is no local neighbor that looks flat. However, if we were to exclude the edges and vertices of the triangle, the subset would be a two-dimensional manifold; thus, \(\{a\vec{h}_1+b\vec{h}_2: a,b > 0, a+b< 1\}\) is a manifold while \(\{a\vec{h}_1+b\vec{h}_2: a,b > 0, a+b\le 1\}\) is not.
6.2.1 Charts, atlases, tangent spaces and approximating tangent planes
Hereafter, we will focus on manifolds which are a subset of \(\mathbb{R}^d\), which are often referred to as submanifolds. Differential geometry can be made far more abstract, but that is unnecessary for the discussion here. After all, we’re dealing with finite dimensional data so any nonlinear surface containing our data must be a submanifold of \(\mathbb{R}^d\)!
Now, some mathematical foundation. Let \(\mathcal{M}\) be a manifold in \(\mathbb{R}^d\) with intrinsic dimension \(t<d\). For every point \(\vec{x}\in\mathcal{M}\), there is a neighborhood \(U_x\subset \mathcal{M}\) containing \(\vec{x}\) and a function \(\phi_x: U_x \to \phi_x(U_x) \subset \mathbb{R}^t\) which is continuous, bijective, and has continuous inverse (a homeomorphism if you like greek). The pair \((U_x,\phi_x)\) is called a chart and behaves much like a map of the area around \(\vec{x}\). There are many choices for \(\phi_x\), but we can always choose one which maps \(\vec{x}\in\mathbb{R}^d\) to the origin in \(\mathbb{R}^t\). For vectors \(\vec{z}\in U_x\), we call \(\phi_x(\vec{z})\in\mathbb{R}^t\) the local coordinates of \(\vec{z}.\)
Example 6.5 (Charts and Manifold Maps) Let’s revisit the swiss roll example from the previous section where \(A = (\pi/2,9\pi/2)\times (0,15)\). We defined the map \(\Psi:A\to \mathbb{R}^3\) as follows \[\Psi(\vec{z}) = \Psi(z_1,z_2) = \begin{bmatrix} z_1\sin(z_1) \\ z_1\cos(z_1) \\ z_2 \end{bmatrix}.\] For other manifolds, we may need multiple charts to cover the manifold, but we only need one chart the swiss roll (or any manifold defined through a homeomorphic manifold map). Let the neighborhood be the entire manifold, i.e. \(U = \mathcal{M}\) Given \(\vec{x}=(x_1,x_2,x_3)^T\), let \(\phi(\vec{x}) = (\sqrt(x_1^2+x_2^2),x_3)^T.\) This chart essentially unrolls the swiss roll and turns it back into a rectangle in \(\mathbb{R}^2\) so that the local coordinates are the original coordinates!
If we take a collection of charts \(\{U_x,\phi_x\}_{x \in \mathcal{I}}\) such that \(\cup_{x\in\mathcal{I}}U_i = \mathcal{M}\), we have at atlas for the manifold. Here \(\mathcal{I}\) is a subset of \(\mathcal{M}\) which could be countable or finite. With a chart, we can consider doing differential calculus on the manifold. In particular, if \(f:\mathcal{M}\to\mathbb{R}\), then for a chart \((U_x,\phi_x)\), the function \(f\circ \phi_x^{-1}\) is a map from a subset of \(\mathbb{R}^t\) (namely \(\phi_x(U)\)) to \(\mathbb{R}\) so we might hope that we could apply the typical rules of calculus. However, if we have two charts \((U_y,\phi_y)\) and \((U_x,\phi_x)\) which overlap – \((U_x\cap U_y) \ne \emptyset\) – then derivatives \(f\circ \phi_x^{-1}\) and \(f\circ \phi_y^{-1}\) should agree on \(U_x\cap U_y\). More succinctly, the rules of calculus should remain consistent across charts!
Definition 6.3 (Differentiable Manifolds) An atlas \(\{U_x,\phi_x\}_{x\in\mathcal{M}}\) is differentiable if the transition maps \(\phi_x \circ \phi_y^{-1}: \phi_y(U_y) \to \mathbb{R}^t\) are differentiable functions. Recall \(\phi_y(U_y)\subset\mathbb{R}^t\) so differentiable in this case follows the traditional Euclidean definition from calculus.
With some additional properties and manifold with a differential atlas is a differentiable manifold allowing us to compute derivatives of function from the manifold to the reals. We’ll revisit this detail again when discussion Hessian Local Linear Embeddings. For now, let’s assume we have a differentiable manifold with intrinsic dimension \(t\). To every point on the manifold, we can attach a \(t\)-dimensional tangent space. There are several methods for defining the tangent space, but the most straightforward involves the case where we have a manifold map. We’ll restrict our attention to this case.
Definition 6.4 (Tangent Space) Let \(A\subset\mathbb{R}^t\) and let \(\Psi:A\to \mathcal{M}\subset \mathbb{R}^d\). Furthermore, suppose \(\Psi\) has coordinate functions \(\Psi_1,\dots,\Psi_d: A \to \mathbb{R}\) such that for \(\vec{y}=(y_1,\dots,y_t)^T\in A\), \(\Psi(\vec{y}) = (\Psi_1(\vec{y}),\dots,\Psi_d(\vec{y}))^T.\) The Jacobian of \(\Psi\), denoted \({\bf J}_{\Psi}\) is the \(d\times t\) dimensional matrix of partial derivative such that \[({\bf J}_{\Psi})_{ij} = \frac{\partial \Psi_i}{\partial y_j}.\] The tangent space of the manifold \(\mathcal{M}\) at the point \(\vec{p}=\Psi(\vec{y})\), denoted \(T_p(\mathcal{M})\) is the column span of \(({\bf J}_{\Psi})\) evaluated at \(\vec{y}\).
The manifold locally resembles \(\mathbb{R}^t\) so the tangent space should also be \(t\)-dimensional. As such, we’ll require \({\bf J}_{\Psi}\) to be a full rank matrix (with rank \(t\) since \(t < d\)) for every \(\vec{y}\in A\). Importantly, the tangent space is a linear subspace meaning it passes through the origin. This should not be confused with tangent plane to the manifold which we now define.
Definition 6.5 (Tangent Plane) Suppose a manifold \(\mathcal{M}\) has tangent space \(T_p(\mathcal{M})\). Then the approximating tangent plane to the manifold is the affine subspace obtained by translations, namely \(\{\vec{x}\in\mathbb{R}^d: \vec{x}-\vec{p} \in T_p(\mathcal{M})\}.\)
Let’s return to the swiss roll to make these details explicit.
Example 6.6 (Jacobians and Tangent Space for the Swiss Roll) The Jacobian of the swiss roll map is \[{\bf J}_{\Psi} = \begin{bmatrix} z_1\cos(z_1) + \sin(z_1) & 0 \\ -z_1\sin(z_1) + \cos(z_1) & 0 \\ 0 & 1 \end{bmatrix}.\] At the point \(\Psi(3\pi/2,5)=(-3\pi/2,0,5)^T\) the Jacobian is \[{\bf J}_{\Psi}\mid_{(3\pi/2,5)^T} = \begin{bmatrix} -1 & 0 \\ -3\pi/2 & 0 \\ 0 & 1 \end{bmatrix}\] so \[T_{(3\pi/2,0,5)^T}(\mathcal{M}) = \text{span}\{(1,3\pi/2,0)^T, (0,0,1)^T\}.\] We can view the associated approximating tangent plane (translucent blue) at the point \((3\pi/2,0,5)^T\) (in red).