Chapter 2 Mathematical Background and Notation

This text assumes a familiarity with probability theory, multivariable calculus, and linear algebra consistent with what one would see in an undergraduate course. The most important concepts are

  • Probability:
    • Major concepts: mean, covariance, correlation, (in)dependence
    • Minor concepts: likelihood functions, conditional expectation, parametric distributions (e.g. Gaussian)
  • Linear Algebra
    • Major concepts: interpretations of matrix-vector and matrix-matrix multiplication, spans, bases, matrix decompositions
    • Minor concepts: orthonormal transformations, vector and matrix norms, Hadamard operations
  • Multivariable calculus:
    • Major concepts: gradients (computation and interpretation), optimization with and without constraints
    • Minor concepts: multivariate Taylor expansions, determing properties of local optima via Hessian matrix

In this chapter, we will identify common notation and review the most important prerequisite material.

2.1 Important notation

Throughout this text, we will be working with vectors and matrices quite often so we begin with a bit of notation and a few important conventions we will adopt hereafter. We’ll use notation \(\vec{x}\in\mathbb{R}^d\) to denote a \(d\)-dimensional vector. Importantly, we adopt the convention that vectors are columns vectors by default so that \[\vec{x} = \begin{bmatrix} x_1 \\ \vdots \\ x_d \end{bmatrix}\] where \(x_1,\dots,x_d\) are the entries or coordinates of vector \(\vec{x}\). Row vectors are then the transpose of column vectors so that \(\vec{x}^T = (x_1,\dots, x_d)\). When needed we’ll let \(\vec{0}\) denote a vector of all zeros and \(\vec{1}\) a vector of all ones with the dimensionality defined implicitly, e.g. if \(\vec{x}\in\mathbb{R}^d\) then in the expression \(\vec{x} + \vec{1}\), you may interpret \(\vec{1}\in\mathbb{R}^d\) so the summation is well defined.

Matrices will be denoted in bold so that \({\bf A}\in\mathbb{R}^{m\times n}\) denotes an \(m\times n\) matrix with real entries. Subscripts are read as row,column so that \({\bf A}_{ij}\) is the entry of \({\bf A}\) in the \(i\)th row and \(j\)th column. A superscript \(T\) denotes the transpose of a matrix. For a square matrix \({\bf B}\in \mathbb{R}^{n\times n}\), we use notation \(Tr({\bf B})\) to denote the trace of \({\bf B}\) and \(det({\bf B}) = |{\bf B}|\) to denotes its determinant.

Using this above notation, we may also define the inner product and outer product of two vectors. For vectors \(\vec{x}\) and \(\vec{y}\), the inner product or dot product of \(\vec{x}\) and \(\vec{y}\) is the scalar \(\vec{x}^T \vec{y} = \sum_{i=1}^d x_i y_i\). Alternatively, we may also consider the outer product \(\vec{x}\vec{y}^T\) which is a matrix such that \((\vec{x} \vec{y}^T)_{ij} = x_i y_j.\) For the inner product to be well defined \(\vec{x}\) and \(\vec{y}\) must have the same dimension. This is not the case for the outer product. If \(\vec{x}\in\mathbb{R}^m\) and \(\vec{y}\in\mathbb{R}^n\) then \(\vec{x} \vec{y}^T \in \mathbb{R}^{m\times n}.\) If we view a \(d\)-dimensional vector as a \(d\times 1\) matrix, then both of these algebraic computations are completely consistent with standard matrix multiplication which we will revisit near the end of this chapter.

Let \(f:\mathbb{R}^d\to \mathbb{R}\) be a function of \(d\)-dimensional vector \(\vec{x}\). Then we define the gradient of \(f\) with respect to \(\vec{x}\), denoted \(\nabla f\), to be the \(d\)-dimensional vector of partial deriviates of \(f\) with respect to the coordinates of \(\vec{x}\) so that \[\nabla f = \begin{bmatrix} \frac{\partial f}{ \partial x_1} \\ \vdots \\ \frac{\partial f}{\partial x_d} \end{bmatrix}.\] The Hessian matrix of \(f\) with respect to \(\vec{x}\), denoted as \(\mathcal{H}f\), is the \(d\times d\) matrix of second order partial derivatives of \(f\) with respect to the coordinates of \(\vec{x}\) so that \((\mathcal{H}f)_{ij} = \frac{\partial^2 f}{\partial x_i \partial x_j}\). If we are considering a function of multiple vector valued variables, e.g. \(f(\vec{x},\vec{y},\vec{z})\) then we use \(\nabla_{\vec{x}}\) to denote the gradient of \(f\) w.r.t. the vector \(\vec{x}\) only.

2.2 Random vectors in \(\mathbb{R}^d\)

Throughout this text, we will consider independent, identically distributed (iid) samples of a \(d\)-dimensional random vector \(\vec{x} = (x_1,\dots,x_d)^T\). Each coordinate \(x_i\) is a random variable and we may view the distribution of the random vector \(\vec{x}\) as the joint distribution of all of its coordinates. The cumulative distribution function of \(\vec{x}\) is then \[F(\vec{x} \le \vec{x}^o\,) = P(\vec{x} \le \vec{x}^o\,) = P(x_1\le x_1^o, \dots ,x_d \le x_d^o\,).\] We’ll largely consider continuous entries so we can rewrite the above in terms of the joint density, \(f: \mathbb{R}^d \to [0,\infty)\), of \(\vec{x}\) such that \[F(\vec{x} \le \vec{x}^o\,) = \int_{-\infty}^{x_1^o}\dots\int_{-\infty}^{x_d^o} f(x_1,\dots,x_d) dx_d\dots dx_1.\] To simplify notation, we’ll often write the above as \[\int_{-\infty}^{x_1^o}\dots\int_{-\infty}^{x_d^o} f(x_1,\dots,x_d) dx_d\dots dx_1 = \int_{-\infty}^{\vec{x}^0} f(\vec{x})d\vec{x}.\] In the case that \(\vec{x}\) may only take one of a countable set of outcomes, one can replace the integral above with a corresponding summation.

Generally speaking we will be considering data drawn from an unknown distribution. However, considering known cases which we can analyze and sample from is often helpful to study how different algorithms perform. With this idea in mind, let’s define a few different distributions which we will revisit throughout this chapter as examples. In each case, we will also provide scatterplots of independent samples from these distributions so that you can visualize the distributions more directly.

Definition 2.1 (Multivariate Gaussian Distribution) The multivariate Gaussian distribution in \(\mathbb{R}^d\) with mean \(\vec{\mu} \in \mathbb{R}^d\) and symmetric positive definite covariance matrix \({\bf \Sigma} \in \mathbb{R}^{d\times d}\) is the random \(d\)-dimensional vector \(\vec{x}\) with probability density function \[f(\vec{x}) = \frac{1}{(2\pi)^{d/2} det({\bf \Sigma})^{1/2}}\exp\left(-\frac{1}{2}(\vec{x}-\vec{\mu})^T{\bf \Sigma}^{-1}(\vec{x}-\vec{\mu})\right).\] We use shorthand \(\vec{x}\sim \mathcal{N}(\vec{\mu},{\bf \Sigma})\) to indicate \(\vec{x}\) follows this distribution.

The Multivariate Gaussian distribution is also often called the Multivariate Normal (MVN) distribution.

For example of the MVN, first consider the two-dimensional case with \(\vec{\mu} = \vec{0}\) and \[{\bf \Sigma} = \begin{bmatrix}1 & p \\ p & 1\end{bmatrix}.\] Below, we show scatterplots of \(1000\) independent samples from this distribution for three different values of \(p.\) We will also refer to a collection of points in \(\mathbb{R}^d\) as a point cloud.

For an examples in \(\mathbb{R}^3\) we again consider case where \(\vec{\mu}=0\) and let \[{\bf \Sigma} = \begin{bmatrix}1 & p & p^2 \\ p & 1 &p \\ p^2 &p & 1 \end{bmatrix}.\]

In the preceding examples, different choices of \(p\), hence different covariance matrices, resulted in point clouds with different orientations and shapes. Later, we’ll discuss how we can determine the shape and orientation from the covariance matrix with the aid of linear algebra. What about changes to \(\vec{\mu}\)? Changing \(\vec{\mu}\) translates the point cloud. If in the preceding examples, we had taken \(\vec{\mu}=\vec{1}\) the scatterplots would have had the same shape and orientation, but they would have been tranlated by a shift of \(\vec{1}.\)

Definition 2.2 (Multivariate t Distribution) The multivariate t-distribution on \(\mathbb{R}^d\) with location vector \(\vec{\mu}\in\mathbb{R}^d\), positive definite scale matrix \({\bf \Sigma}\in \mathbb{R}^{d\times d}\) and degrees of freedom \(\nu\) has density \[f(\vec{x}) = \frac{\Gamma\left(\frac{\nu+d}{2}\right)}{\Gamma(\nu/2)\nu^{d/2}\pi^{d/2}|{\bf \Sigma}|^{1/2}}\left[1 + \frac{1}{\nu}(\vec{x}-\vec{\mu})^T{\bf \Sigma}^{-1}(\vec{x}-\vec{\mu})\right]^{-(\nu +d)/2}.\] We use shorthand \(\vec{x}\sim t_\nu(\vec{\mu},{\bf \Sigma})\) to indicate \(\vec{x}\) follows this distribution.

We’ll only consider a three dimensional case where the location, which determines the mode of the distribution, is \(\vec{0}\) and the scale is the identity matrix. As in the Gaussian case, changing \(\vec{\mu}\) translates the point cloud and different values of \({\bf \Sigma}\) give point clouds with different shapes. The remaining parameter to consider here is the degrees of freedom, \(\nu\), which controls how spread out the samples can be. We show results for three different choices of the degrees of freedom. For smaller degrees of freedom, there are more points which are far from the mode at \(\vec{0}\).

2.3 Expectation, Mean, and Covariance

As in the one-dimensional case, the cumulative distribution function determines the distribution of the random vector, and using the density we may establish a few important quantities which will appear often throughout this text.

The first is the mean or expected value of the random vector which is the vector of expected values of each entry so that \[\begin{equation} E[\vec{x}] = \int_{\mathbb{R}^d}\vec{x} f(\vec{x})d\vec{x} = \begin{bmatrix} E[x_1] \\ \vdots \\ E[x_d] \end{bmatrix} = \begin{bmatrix} \int_{\mathbb{R}^d} x_1 f(\vec{x})d\vec{x} \\ \vdots \\ \int_{\mathbb{R}^d} x_d f(\vec{x})d\vec{x} \end{bmatrix} \tag{2.1} \end{equation}\] where \[\int_{\mathbb{R}^d} x_i f(\vec{x})d\vec{x} = \int_{-\infty}^\infty \dots \int_{-\infty}^\infty x_i f(x_1,\dots,x_d)dx_1 \dots dx_d.\] Note, we are assuming each of the integrals in (2.1) is well defined, which is a convention we adhere to throughout this text. Often, we’ll often use \(\vec{\mu}\) to denote the mean vector. When we are considering more than multiple random vectors \(\vec{x}\) and \(\vec{y}\) we will add a corresponding subscript \(\vec{\mu}_{\vec{x}}\) to denote the corresponding mean of \(\vec{x}\).

The linearity of expectation for univariate random vectors holds here as well. If \(\vec{x}\in\mathbb{R}^d\) is a random vector, \({\bf A}\in\mathbb{R}^{k\times d}\) is a matrix of constant entries, and \(\vec{b}\in\mathbb{R}^k\) is a vector of constant entries then \[E[{\bf A}\vec{x} + \vec{b}] = {\bf A}\vec{\mu} + \vec{b}.\] Importantly, for non-squared matrices \({\bf A}\) then mean of \({\bf A}\vec{x}\) will be of a different dimension than \(\vec{x}.\)

In general, the coordinates of a random vector will not be independent. To quantify the pairwise dependence, we could consider the covariance \[Cov(x_i,x_j) = E[(x_i - \mu_i)(x_j -\mu_j)] = \int_{\mathbb{R}^d} (x_i-\mu_i)(x_j-\mu_j) f(\vec{x})d\vec{x}\] for \(1\le i,j \le d\). In the case \(i=j\), this simplifies to \(Cov(x_i,x_i) = Var(x_i)\).

Importantly, we do not want to consider each all of the pairwise covariance separately. Instead, we can organize them as a \(d\times d\) matrix \({\bf \Sigma}\) with entries \({\bf \Sigma}_{ij} = Cov(x_i,x_j)\). Hereafter, we will refer to \({\bf \Sigma}\) as the covariance matrix of \(\vec{x}.\) When we are considering multiple random vectors we will use subscripts so that \({\bf \Sigma}_{\vec{x}}\) and \({\bf \Sigma}_{\vec{y}}\) denote the covariance matrices or random vectors \({\vec{x}}\) and \({\vec{y}}\) respectively. Following the notational conventions, it follows that \(\vec{x} - E[\vec{x}] = \vec{x} - \vec{\mu} \in \mathbb{R}^d\) so that the outer product of \(\vec{x} - \vec{\mu}\) with itself is the \(d\times d\) matrix with entries \[[(\vec{x} - \vec{\mu})(\vec{x} - \vec{\mu})^T]_{ij} = (x_i-\mu_i)(x_j-\mu_j)\] so that we may more compactly write \[\begin{equation} \text{Var}(\vec{x}) = E\left[(\vec{x} - \vec{\mu})(\vec{x} - \vec{\mu})^T\right] \tag{2.2} \end{equation}\] where we interpret the expectation operation as applying to each entry of the matrix \((\vec{x} - \vec{\mu})(\vec{x} - \vec{\mu})^T\). This looks very similar to the univariate case save that we must be mindful of the multidimensional nature of our random vector. In fact with some algebra, we have the following alternative formula for the covariance matrix \[{\bf \Sigma} = E[\vec{x}\,\vec{x}^T] -\vec{\mu}\vec{\mu}^T\] which is again reminiscent of the univariate case. Showing this result is left as a short exercise. One brief note to avoid confusion. Other texts refer to \(\text{Var}(\vec{x})\) as the variance matrix or variance-covariance matrix. Herein, we use the term covariance matrix for \(\text{Var}(\vec{x}).\)

Recall the univariate case, \[\text{Var}(aX+b) = a^2\text{Var}(X)\] for constants \(a\) and \(b\) and (one-dimensional) random variable \(X\). Similar to the univariate case, there is a formula for the covariance of an affine mapping of a random vector, but the specific form requires us to be mindful of the matrix structure of the covariance matrix. For random vector \(\vec{x}\in\mathbb{R}^d\), constant matrix \({\bf A}\in\mathbb{R}^{k\times d}\) and constant vector \(\vec{b}\in\mathbb{R}^k\), it follows (see exercises) that \[{\bf \Sigma}_{{\bf A}\vec{x}+\vec{b}} = {\bf A \Sigma A}^T.\] Importantly, note that \({\bf A \Sigma A}^T\) is a \(k\times k\) matrix which is consistent with the fact that \({\bf A}\vec{y}+\vec{b}\) is a \(k\)-dimensional vector.

Example 2.1 (Mean and Covariance of MVN) If \(\vec{x} \sim \mathcal{N}(\vec{\mu}, {\bf \Sigma})\) then \(E[\vec{x}] = \vec{\mu}\) and \(\text{Var}(\vec{x}) = {\bf \Sigma}\)

Example 2.2 (Mean and Covariance of Multivariate t-distribution) Let \(\vec{x} \sim t_\nu(\vec{\mu}, {\bf \Sigma})\). If \(\nu > 1\) then \(E[\vec{x}] = \vec{\mu}\); otherwise the mean does not exist. If \(\nu > 2\), then \(\text{Var}(\vec{x}) = \frac{\nu}{\nu-2}{\bf \Sigma}\); otherwise, the covariance matrix does not exist.

Verifying these examples is left to the exercises and rely on multivariate change of variables which are not covered here.

2.3.1 Sample Mean and Sample Covariance

In many cases, we’ll consider a collection of \(N\) \(iid\) vectors \(\vec{x}_1,\dots,\vec{x}_N \in \mathbb{R}\). Again, subscripts are used here, but importantly when accompanied by the \(\vec{\cdot}\) sign a subscript does not refer to a specific coordinate of a vector but rather one vector in a set. Given iid observations \(\vec{x}_1,\dots,\vec{x}_N\), we will use sample averages to estimate the expectation and covariance of the data generating distribution. We’ll use bars to denote sample averages so that \(\bar{x}\) denotes the sample mean and \(\bar{\bf \Sigma}\) the sample covariance. In this case, we have \[\begin{equation} \bar{x} = \frac{1}{N}\sum_{i=1}^N \vec{x}_i. \tag{2.3} \end{equation}\]

Similarly, we define the sample covariance matrix to be \[\begin{equation} {\bf \bar{\Sigma}} = \frac{1}{N} \sum_{i=1}^N (\vec{x}_i - \bar{x})(\vec{x}_i - \bar{X})^T = \left(\frac{1}{N}\sum_{i=1}^N \vec{x}_i\vec{x}_i^T\right) - \bar{x}\bar{x}^T \tag{2.4} \end{equation}\] In (2.4), dividing by \(N\) rather than \(N-1\) yields biased estimates of the terms of the sample covariance matrix. However, the final formula in (2.4) more directly matches the corresponding term in the definition of the covariance matrix. Had we used a factor of \(1/(N-1)\) instead, we would have \[\frac{1}{N-1}\sum_{i=1}^N (\vec{x}_i - \bar{X})(\vec{x}_i - \bar{X})^T = \left(\frac{1}{N}\sum_{i=1}^N \vec{x}_i\vec{x}_i^T\right) - \frac{N}{N-1}\bar{x}\bar{x}^T\] which is slightly more cumbersome. In the examples we will consider, \(N\) will typically be large enough so that the numerical difference is small. As such, we will opt for algebraically convenient definition form of (2.4) as our definition of the sample covariance matrix.

Alternatively, we can view the sample mean and sample covariance as the mean and covariance (using expectation rather than averages) of the empirical distribution from a collection of samples \(\vec{x}_1,\dots,\vec{x}_N\) defined below.

Definition 2.3 (Empirical Distribution) Given a finite set of points \(\mathcal{X}=\{\vec{x}_1,\dots,\vec{x}_N\} \subset \mathbb{R}^d\), we say that random vector \(\vec{z}\) follows the empirical distribution from data \(\mathcal{X}\) if \[P(\vec{z} = \vec{x}_i) = \frac{1}{N}, \quad i = 1,\dots, N\] and is zero otherwise.

If \(\vec{z}\) follows the empirical distribution on a set of \(N\) points \(\mathcal{X}= \{\vec{x}_1,\dots,\vec{x}_N\}\), then the expectation and covariance matrix of \(\vec{z}\) are equivalent to the sample mean and sample covariance for data \(\vec{x}_1,\dots,\vec{x}_N.\)

2.3.2 The Data Matrix

Both (2.3) and (2.4) involve summations. Working with sums will prove cumbersome, so briefly let us introduce a more compact method for representing these expressions. Hereafter, we will organize the vectors \(\vec{x}_1,\dots, \vec{x}_N\) into a data matrix \[{\bf X} = \begin{bmatrix} \vec{x}_1^T \\ \vdots \\ \vec{x}_N^T\end{bmatrix} \in \mathbb{R}^{N\times d}.\] In this setup, \({\bf X}_{ij}\) is the \(j\)th coordinate of \(\vec{x}_i\), or equivalently, the \(j\)th measurement taken from the \(i\)th subject. Thus, rows of \({\bf X}\) index subjects (realizations of the random vector) whereas columns index common measurements across all subjects. Using the data matrix, we can forgo the summation notation giving the following formulas for the sample mean \[\begin{equation} \bar{x} = \frac{1}{N} {\bf X}^T \vec{1} \tag{2.5} \end{equation}\] and the sample covariace matrix \[\begin{equation} {\bf \bar{\Sigma}} = \frac{1}{N} ({\bf HX})^T {\bf HX} = \frac{1}{N} {\bf X}^T {\bf H X} \tag{2.6} \end{equation}\] where \({\bf H} = {\bf I} - \frac{1}{N} \vec{1} \vec{1}^T \in \mathbb{R}^{N\times N}\) is known as the centering matrix. We have used the fact that \({\bf H}\) is symmetric and idempotent, e.g. \({\bf H}^2 = {\bf H}\) which is left as a exercise. The vector \(\vec{1}\) is the \(N\)-dimensional vector with 1 in each entry and \({\bf I}\) is the \(N\times N\) identity matrix. One can show (see exercises) that the matrix-vector and matrix-matrix multiplication implicitly handles the summations in (2.3) and (2.4).

To conclude this section, we compare the sample mean and covariance matrix computed from random draws from the \(MVN\) distribution.

Example 2.3 (Draws from the MVN) We draw \(N=100\) samples from the \(\mathcal{N}(\vec{0}, {\bf \Sigma})\) distribution where \[{\bf \Sigma}=\begin{bmatrix}1 & 0 & 0 \\ 0 &4 & 0 \\ 0&0&9\end{bmatrix}\].

N <- 100
X <- mvrnorm(n=N, mu = rep(0,3), Sigma = c(1,4,9)*diag(3))

To compute the sample mean and sample covariance, we implement (2.3) and (2.4).

xbar <- (1/N) * t(X) %*% rep(1,N)
H <- diag(N) - (1/N)*matrix(1,nrow = N, ncol = N)
S <- (1/N) *  t(H %*% X) %*% (H %*% X)

The results are shown below (rounded to three decimal places) \[\bar{x} = \begin{bmatrix} 0.008 \\ 0.078 \\ -0.239 \end{bmatrix} \qquad \text{and} \qquad \bar{\bf \Sigma} = \begin{bmatrix} 1.148 & 0.216 & 0.121 \\ 0.216 & 4.181 & 0.087 \\ 0.121 & 0.087 & 9.366 \end{bmatrix}\]

which are close to the true values. If we increase the sample size to \(N=10^4\) samples, we get estimates which are closer to the true values (shown below).

\[\bar{x} = \begin{bmatrix} 0.001 \\ 0.02 \\ 0.051 \end{bmatrix} \qquad \text{and} \qquad \bar{\bf \Sigma} = \begin{bmatrix} 0.991 & -0.02 & -0.04 \\ -0.02 & 3.997 & 0.095 \\ -0.04 & 0.095 & 8.992 \end{bmatrix}\]

2.4 Linear Algebra

2.4.1 Assumed Background

This text assumes familiarity with definitions from a standard undergraduate course in linear algebra including but not limited to linear spaces, subspaces, spans and bases, and matrix multiplication. However, we have elected to provide review of some of the most commonly used ideas in the methods we’ll cover in the following subsections. For a more thorough treatment of linear algebra, please see [5]

2.4.2 Interpretations of Matrix Multiplication

Throughout this text, comfort with common calculations in linear algebra will be very important. Herein, we assume the reader has some exposure to these materials at an undergraduate level including the summation of vectors or matrices. The familiarity with matrix-vector and matrix-matrix multiplication will play a central role as we have already seen in the case of the data matrix formulation of the sample mean and sample covariance. However, rote familiarity with computation will not be sufficient to build intuition for the methods we’ll discuss. As such, we’ll begin with a review of a few important ways one can view matrix-vector (and matrix-matrix) multiplication which will be helpful later. Those who feel comfortable with the myriad interpretations of matrix multiplication in terms of linear combinations of the rows and columns may skip to the next section.

Suppose we have matrix \({\bf A}\in\mathbb{R}^{m\times n}\) and vector \(\vec{x}\in\mathbb{R}^n\). If we let \(\vec{a}_1^T,\dots, \vec{a}_M^T\in\mathbb{R}^n\) denote the rows of \({\bf A}\), then the most commonly cited formula for computing \({\bf A}\vec{x}\) is \[{\bf A}\vec{x} = \begin{bmatrix} \vec{a}_1^T \\ \vdots \\ \vec{a}_m^T\end{bmatrix} \vec{x} = \begin{bmatrix}\vec{a}_1^T \vec{x} \\ \vdots \\ \vec{a}_m^T\vec{x}\end{bmatrix}\] wherein we take the inner product of the rows of \({\bf A}\) with vector \(\vec{x}\). We can expand this definition to matrix-matrix multiplication. If \({\bf B}\in\mathbb{R}^{n\times k}\) has columns \(\vec{b}_1,\dots,\vec{b}_k\) then \[({\bf AB})_{ij} = \vec{a}_i^T\vec{b}_j\] where we take the inner product of the \(i\)th row of \({\bf A}\) with the \(j\)th column of \({\bf B}\) to get the \(ij\)th entry of \({\bf AB}.\) This is perfectly reasonable method of computation, but alternative perspectives are helpful, particularly when we consider different factorization of the data matrix in later chapters..

Returning to \({\bf A}\vec{x}\), suppose now that \({\bf A}\) has columns \(\vec{\alpha}_1,\dots,\vec{\alpha}_n\) and \(\vec{x} = (x_1,\dots,x_n)^T\), then we may view \({\bf A}\vec{x}\) as a linear combination of the columns of \({\bf A}\) so that \[{\bf A}\vec{x} = \begin{bmatrix}\vec{\alpha}_1 \,| & \cdots &|\, \vec{\alpha}_n \end{bmatrix} \begin{bmatrix} x_1 \\ \vdots \\ x_n \end{bmatrix} = x_1\vec{\alpha}_1 + \dots + x_n \vec{\alpha}_n = \sum_{j=1}^n x_j\vec{\alpha}_j.\] Here, we added vertical columns between the vectors \(\vec{\alpha}_i\) to make clear that \(\begin{bmatrix}\vec{\alpha}_1 \,| & \cdots &|\, \vec{\alpha}_n \end{bmatrix}\) is a matrix. We can extend this perspective to see that the columns of \({\bf AB}\) are comprised of different linear combinations of the columns of \({\bf A}\). Specifically, the \(j\) column of \({\bf AB}\) is a linear combination of the columns of \({\bf A}\) using the entries in the \(j\)th column of \({\bf B}\). More specifically, the \(j\)th column of \({\bf AB}\) is the linear combination \[\sum_{i=1}^n {\bf B}_{ij}\vec{\alpha}_{i}.\]

Our final observations follows by taking these insights on linear combinations of columns and transposing the entire operation. What can we say about the rows of \({\bf AB}\)? We can rewrite \({\bf AB} = ({\bf B}^T{\bf A}^T)^T\). The columns of \({\bf B}^T{\bf A}^T\) are linear combinations of the columns of \({\bf B}^T\). Since the columns of \({\bf B}^T\) are the rows of \({\bf B}\), it follows that the rows of \({\bf AB} = ({\bf B}^T{\bf A}^T)^T\) are linear combinations of the rows of \({\bf B}\) with weights given by the entries in each row of \({\bf A}\) respectively. In mathematical notation, the \(i\)th row of \({\bf AB}\) is \[\sum_{j=1}^n {\bf A}_{ij} \vec{\beta}_j^T\] where \(\vec{\beta}_1^T,\dots, \vec{\beta}_n^T\) are the rows of \({\bf B}.\)

2.4.3 Norms and Distances

Throughout this text, we will use \(\| \cdot \|\) to denote the usual Euclidean (or \(\ell_2\)) norm, which for a vector, \(\vec{x} = (x_1,\dots,x_d)\in\mathbb{R}^d\), is \[\|\vec{x}\| = \left(\sum_{j=1}^d x_j^2 \right)^{1/2}.\] We may then define the Euclidean distance between two \(d\)-dimension vectors \(\vec{x}\) and \(\vec{y}\) to be \[\|\vec{x}-\vec{y}\| = \left(\sum_{j=1}^d (x_j - y_j)^2\right)^{1/2}.\] Euclidean distance is the most commonly used notion of distance (or norm or metric) between two vectors, but it is far from the only option. We can consider the general \(\ell_p\) norm \[\|\vec{x}\|_p = \left(\sum_{j=1}^d x_j^p\right)^{1/p}\] which coincides with the Euclidean norm for \(p=2\). Two other special cases include \(p=1\) also known as the Manhattan distance and \(p = \infty\) also known as the sup-norm \[\|\vec{x}\|_\infty = \max_{j=1,\dots, d} |x_j|.\]

We can also extend this notions of vector norms to a measure of the norm of a matrix. Two important cases are the \(\ell_2\) norm of a matrix and the Frobenius norm. For matrix \({\bf A}\in\mathbb{R}^{m\times n}\), the \(\ell_2\) norm is \[\begin{equation} \|{\bf A}\| = \sup_{\vec{x}\in\mathbb{R}^n \text{ s.t. } \vec{x}\ne \vec{0}} \frac{\|{\bf A}\vec{x}\|}{\|\vec{x}\|} = \sup_{\vec{x}\in\mathbb{R}^n \text{ s.t. }\|\vec{x}\|=1} \|{\bf A}\vec{x}\|. \end{equation}\] You can interpret \(\|{\bf A}\|\) as the largest relative change in the Euclidean length of a vector after it is multiplied by \({\bf A}\). The Frobenius norm extends the algebraic definition notion of Euclidean length to a matrix. For \({\bf A}\in\mathbb{R}^{m\times n}\), its Frobenius norm is \[\begin{equation} \|{\bf A}\|_F = \left(\sum_{i=1}^m\sum_{j=1}^n {\bf A}_{ij}^2\right)^{1/2}. \end{equation}\] The \(\ell_2\) distance between two matrices is then \(\|{\bf A}-{\bf B}\|\) and the Frobenius distance between two matrices is \(\|{\bf A} - {\bf B}\|_F\) (where both \({\bf A}\) and \({\bf B}\) have the same number of rows and columns).

2.4.4 Important properties

A few additional definitions that we will use throughout the text are provided below without examples.

Definition 2.4 (Symmetric Matric) Matrix \({\bf A}\in \mathbb{R}^{d\times d}\) is symmetric if \({\bf A} = {\bf A}^T.\)

Definition 2.5 (Eigenvectors and Eigenvalues) Let \({\bf A}\in\mathbb{R}^{d\times d}\). If there is a scalar \(\lambda\) and vector \(\vec{x}\ne \vec{0}\) such that \({\bf A}\vec{x} = \lambda \vec{x}\) then we say \(\lambda\) is an eigenvalue of \({\bf A}\) with associated eigenvector \(\vec{x}.\)

2.4.5 Matrix Factorizations

Two different matrix factorization will arise many times throughout the text. The first, which is commonly presented in linear algebra courses, is the spectral decomposition of a square matrix which is also known as diagonalization or eigenvalue decomposition. Herein, we assume familiarity with eigenvalues and eigenvectors. The second factorization is the singular value decomposition. In the subsequent subsections, we briefly discuss these two factorizations, their geometric interpretation, and some notation that will typically be used in each case.

2.4.5.1 Eigenvalue Decomposition

We begin with the eigenvalue decomposition of a square matrix \({\bf A}\in\mathbb{R}^{d\times d}\). As you may recall, \({\bf A}\) will have a set of \(d\) eigenvalues \(\lambda_1,\dots, \lambda_d\) (which may include repeated values) and associated eigenvectors. A number, \(\lambda\), may be repeated in the list of eigenvalues, and the number of times is called the algebraic multiplicity of \(\lambda\). Each eigenvalue has a least one eigenvector. In cases where the eigenvalue has algebraic multiplicity greater than one, we refer to its geometric multiplicity as the number of linearly independent eigenvectors associated with the eigenvalue.

The algebraic multiplicity is always greater than or equal to the geometric multiplicity. However, this is not always the case, and when this occurs, the matrix cannot be diagonalized. Fortunately, we will largely be dealing with symmetric matrices for which diagonalization is guaranteed by the following theorem.

Theorem 2.1 (Spectral Decomposition Theorem for Symmetric Matrices) Any symmetric matrix \({\bf A}\in\mathbb{R}^{d\times d}\) can be written as \[{\bf A} = {\bf U\Lambda U}^T\] where \({\bf U}\in\mathbb{R}^{d\times d}\) is an orthonormal matrix and \({\bf \Lambda}\) is a diagonal matrix \[{\bf \Lambda} = \begin{bmatrix} \lambda_1 & 0&0 \\ 0& \ddots &0 \\ 0&0 &\lambda_d\end{bmatrix}\] where the scalars \(\lambda_1,\dots,\lambda_d \in \mathbb{R}\) are the eigenvalues of \({\bf A}\) and the corresponding columns of \({\bf U}\) are their associated eigenvectors.

By convention, we will always assume the eigenvalues are in decreasing order so that \(\lambda_1\ge \lambda_2 \ge \dots \ge \lambda_d\). The most common types of symmetric matrices that we will encounter are covariance matrices. In those cases, the spectral decomposition of the covariance can provide some helpful insight about the shape generated by many iid samples from a distribution. We demonstrate this idea graphically in the following examples using the MVN.

Example 2.4 (Level curves of MVN in) A scatterplot of 1000 iid samples from two-dimensional Gaussian distribution with mean \(\vec{0}\) and covariance \(\begin{bmatrix} 10& 2 \\ 2 & 10 \end{bmatrix}\) is shown below. The eigenvector associated with the largest eigenvalue of the sample covariance matrix is shown in red, whereas the eigenvector shown associated with the second eigenvalue is shown in blue. Note, both eigenvectors have been rescaled so their length is the square root of the associated eigenvalues.

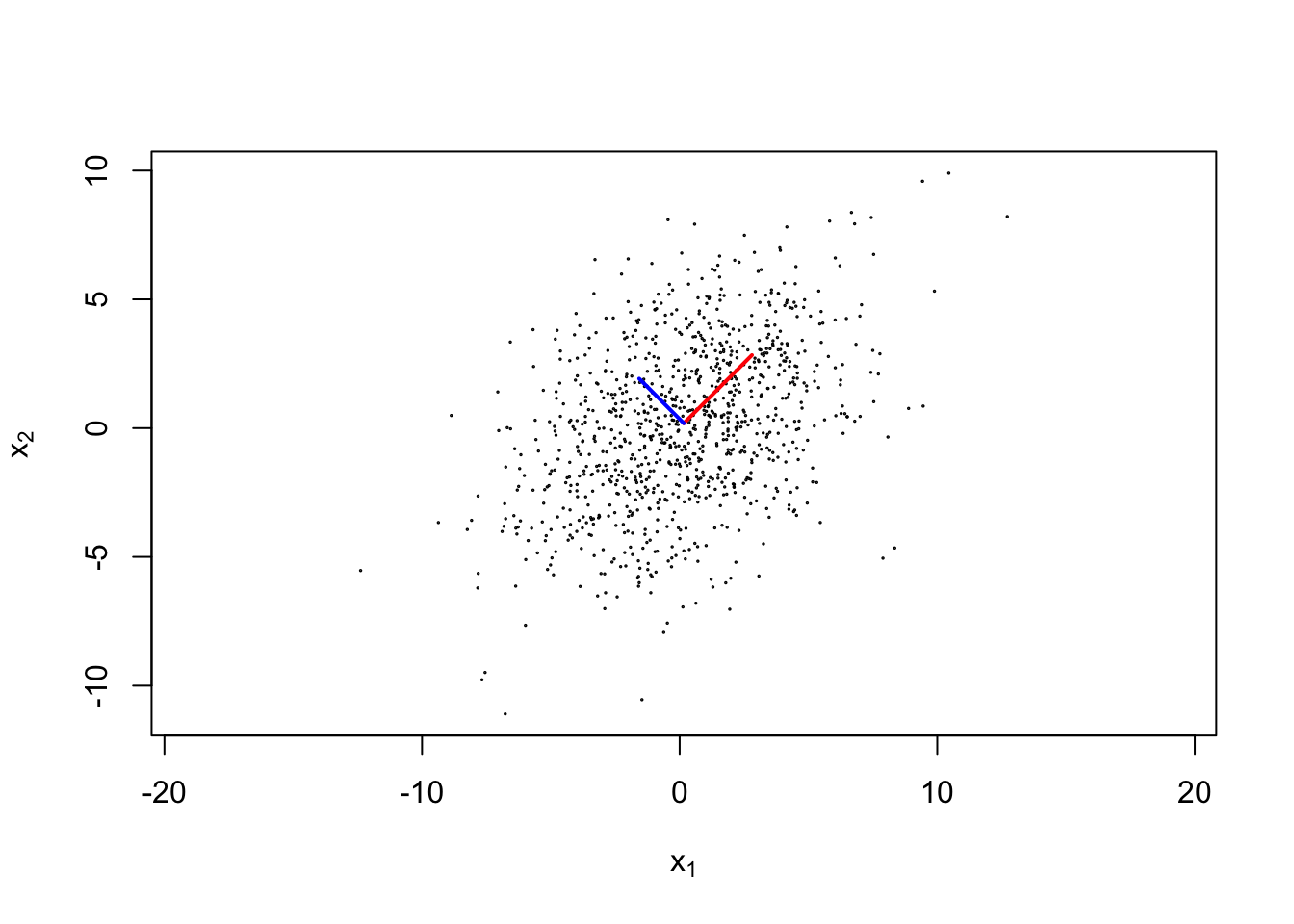
Importantly, observe how these eigenvectors follow the spread of the data. As we will see in 4.1, this idea can be used to compress data in a geometrically interpretable manner through PCA.

2.4.5.2 Singular Value Decomposition

The spectral theorem is limited in that it requires a matrix to be both square and symmetric. When focusing on data matrices \({\bf X}\in\mathbb{R}^{N\times d}\) both assumptions are extremely unlikely to be satisfied, and we will need a more flexible class of methods. This idea is explored in much greater detail in Chapter 4. For now, we briefly introduce the Singular Value Decomposition and how this factorization provides some insight on the geometric structure of matrix-vector multiplication.

For a matrix \({\bf A}\in\mathbb{R}^{m\times n}\) the mapping \(T_{\bf A}: \mathbb{R}^n \mapsto \mathbb{R}^m\) defined as \(T_{\bf A}(\vec{x}) = {\bf A}\vec{x}\) for \(\vec{x}\in\mathbb{R}^n\). Since this mapping is linear, we can understand its geometric nature by investigating how the unit sphere in \(\mathbb{R}^n\) is transformed by the mapping \(T_{\bf A}\). More directly, let’s suppose we took every vector on the unit sphere \(\mathcal{S} = \{\vec{x}\in\mathbb{R}^n \, : \|\vec{x}\| = 1\}\) and computed the vector \({\bf A}\vec{x}\). The result is a hyperellipse in \(\mathbb{R}^m\). The specifics on the orientation and shape of the hyperellipse depend on the matrix \({\bf A}\) which we demonstrate through a brief example.

Example 2.5

In Figure 2.1, we show the unit sphere in \(\mathbb{R}^2\) and the resulting hyperellipse in \(\mathbb{R}^3\) after multiplication by the matrix \[{\bf A} = \begin{bmatrix} 3 & 2 \\ 2&1 \\ 1& 0 \end{bmatrix}.\]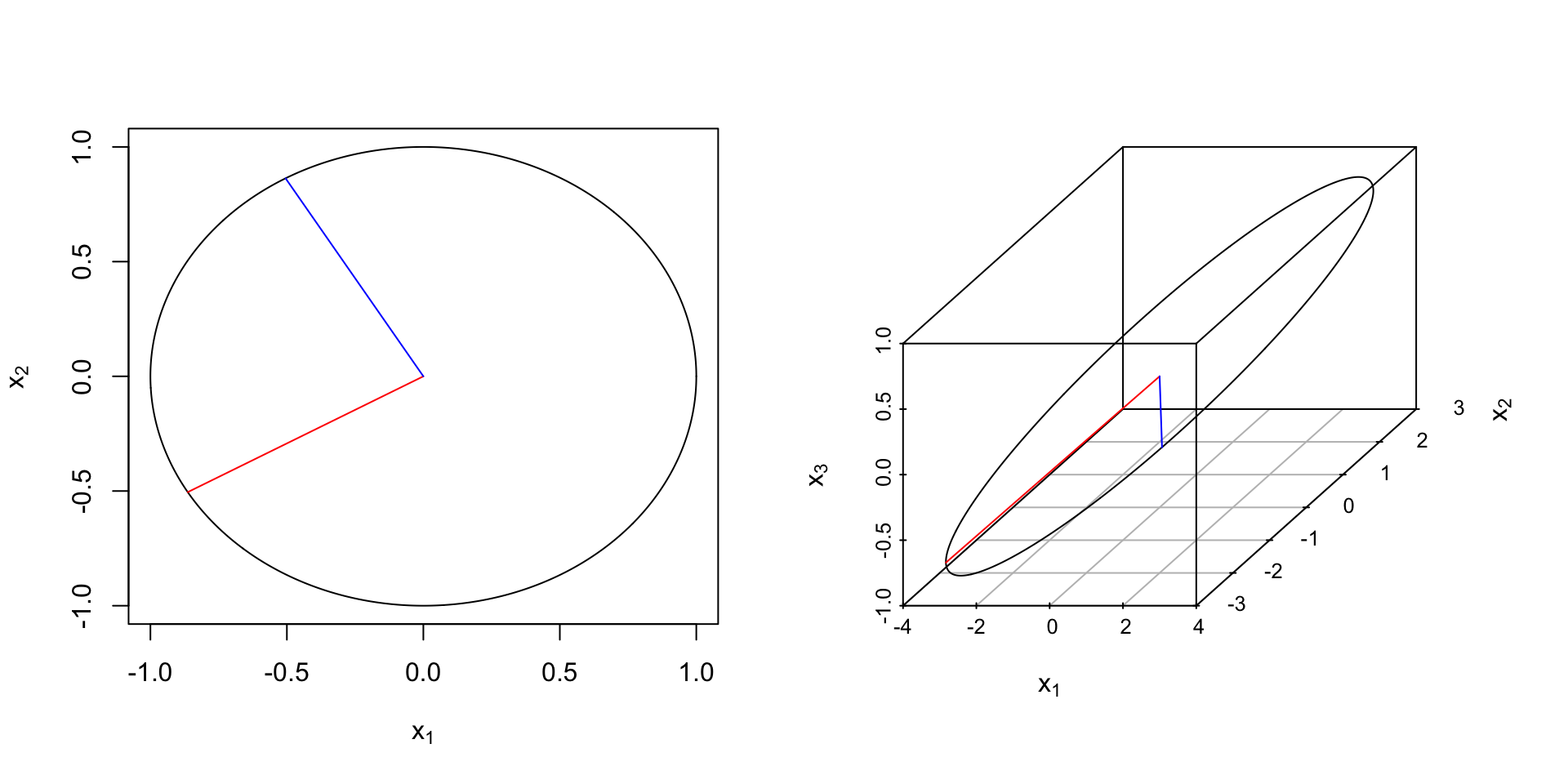
(Left) Unit sphere in 2D, (Right) Hyperellipse that results after multiplication by A

Figure 2.1: (Left) Unit sphere in 2D, (Right) Hyperellipse that results after multiplication by A

We have also added two vectors. On the hyperellipse, the red vector is the longest semi-axis of the ellipse; the blue vector is the shortest semi-axis. The red and blue vectors on the left are the preimages of the semi-axes of the ellipse (those vectors which get mapped to the semi-axes after multiplication with \({\bf A}\)). It may not be clear from the static images above, but the semi-major axes on the right are orthogonal. We provide an interactive plot of hyperellipse below so that you can better see this result. Interestingly, the preimages on the left are also perpendicular. Since they are on the unit sphere, they are also orthonormal.

In the preciding example, we have made a few important observations which generalize to any multiplication by a matrix, \({\bf A}\in\mathbb{R}^{m\times n}\). For now, assume that \(m> n\) and \({\bf A}\) is full rank. In this case, the hyperellipse \({\bf A} \mathcal{S} = \{{\bf A}\vec{x}\, : \vec{x} \in \mathcal{S}\}\) has orthogonal semi-axes \(\sigma_1\vec{u}_1,\dots,\sigma_n\vec{u}_n\) with corresponding orthonormal preimages \(\vec{v}_1,\dots,\vec{v}_n\). We use the assumption that the lengths of the axes are listed in decreasing order so that \(\sigma_1\ge \dots\ge \sigma_n\). We may express these mappings in the following manner

\[\begin{equation} {\bf A}\underbrace{ \begin{bmatrix}\\ \vec{v}_1 |& \dots & |\vec{v}_n \\ &&\end{bmatrix}}_{\tilde{\bf V}} = \begin{bmatrix} \\ \sigma_1 \vec{u}_1 & \dots & \sigma_n\vec{u}_n \\&& \end{bmatrix} = \underbrace{\begin{bmatrix}&& \\ \vec{u}_1 & \dots & \vec{u}_n \\ &&\end{bmatrix}}_{\tilde{\bf U}}\underbrace{ \begin{bmatrix} \sigma_1 & 0& 0\\ 0& \ddots &0 \\ 0&0& \sigma_n \end{bmatrix}}_{\tilde{\bf S}} \end{equation}\]

Since \(\tilde{\bf V} \in \mathbb{R}^{n\times n}\) has orthonormal columns so that \(\tilde{\bf V} ^{-1} = \tilde{\bf V}^T\), we arrive at the following decomposition for \({\bf A}.\)

Definition 2.6 (The Singular Value Decomposition (SVD)) Let \({\bf A} \in \mathbb{R}^{m\times n}\). Then \({\bf A}\) may be factored as \[\begin{equation} {\bf A} = \tilde{\bf U}\tilde{\bf S}\tilde{\bf V}^T \tag{2.7} \end{equation}\] where \(\tilde{\bf U}\in\mathbb{R}^{m\times n}\) and \(\tilde{\bf V}\in\mathbb{R}^{n\times n}\) have orthonormal columns and \(\tilde{\bf S}\in\mathbb{R}^{n\times n}\) is a diagonal matrix with real entries \(\sigma_1 \ge \dots \sigma_n \ge 0\) along the diagonal. We refer to (2.7) as the reduced singular value decomposition of \({\bf A}.\) The columns of \(\tilde{\bf U}\) (\(\tilde{\bf V}\)) are called the left (right) singular vectors of \({\bf A}\) and the scalars \(\sigma_1\ge \dots\ge \sigma_n\) are referred to as the singular values of \({\bf A}.\)

Let \(\vec{u}_1,\dots,\vec{u}_n\in\mathbb{R}^m\) be the columns of \(\tilde{\bf U}\). When \(m > n\), we may find additional vectors \(\vec{u}_{n+1},\dots,\vec{u}_m\) such that \(\{\vec{u}_1,\dots,\vec{u}_m\}\) are an orthonormal basis for \(\mathbb{R}^m\). This gives the (full) singular value decomposition of \({\bf A}\) is \[\begin{equation} {\bf A} = {\bf US\bf V}^T \tag{2.8} \end{equation}\] where \[{\bf U} = \begin{bmatrix} \vec{u}_1 & \dots & \vec{u}_m\end{bmatrix}\in\mathbb{R}^{m\times m} \qquad {\bf V} = \begin{bmatrix} \vec{v}_1 & \dots & \vec{v}_n\end{bmatrix}\in\mathbb{R}^{n\times n}\] are orthonormal matrices. The matrix \({\bf S}\in\mathbb{R}^{m\times n}\) is formed by taking \(\tilde{S}\) and padding it with zero along the bottom and right so that it is \(m\times n\).

We may drop the preceding assumptions that \(m > n\) or the \({\bf A}\) is full rank. In fact, every matrix has a singular value decomposition. A proof of this fact using induction may be found in [4]. Furthermore, a few important matrix properties are directly related to the SVD.

  1. The rank of a matrix is equal to its number of positive singular values
  2. The column space of a matrix is the span of its first \(rank({\bf A})\) left singular vectors
  3. The kernel of a matrix is the span of its last \(n-rank({\bf A})\) right singular vectors.

When considering matrix muliplication \({\bf A}\vec{x}\), the full SVD of \({\bf A}\) is helpful for decomposition this matrix multiplication into three more interpretable steps: a rotation/reflection, a stretch/compression, and a final rotation/reflection.

\[\begin{equation} {\bf A}\vec{x} =\underbrace{ {\bf U} \underbrace{[{\bf D} \underbrace{({\bf V}^T \vec{x} )}_{rot/ref}]}_{str/com}}_{rot/ref} \end{equation}\]

2.4.6 Positive Definiteness and Matrix Powers

Finally, we review a few brief properties for square matrices.

Definition 2.7 (Positive Definite Matrices) A matrix, \({\bf A}\in\mathbb{R}^{n\times n}\) is positive definite if \(\vec{x}^T{\bf A}\vec{x} >0\) for all \(\vec{x}\ne 0.\) Equivalently, \({\bf A}\) is positive definite if all of its eigenvalues are positive.

A matrix is positive semidefinite if \(\vec{x}^T{\bf A}\vec{x} \ge 0\) for all \(\vec{x}\ne 0.\) Equivalently, \({\bf A}\) is positive semidefinite if all of its eigenvalues are non-negative.

One may interpret the powers of a matrix as repeated multiplication of a square matrix. More specifically, for any \(m\in \{1,2,\dots\}\), let \({\bf A}^m = \underbrace{{\bf A} \dots {\bf A}}_{m \text{ times}}\). For diagonalizable positive definite matrices, we may extend this interpretation to negative and fractional power using the eigenvalue decomposition. If the eigenvalue decomposition of the \({\bf A}\) is \({\bf A} = {\bf W \Lambda W}^{-1}\) for some diagonal matrix \({\Lambda}\) with positive entries, \(\lambda_1,\dots,\lambda_n\) along its diagonal. For any \(s\in\mathbb{R}\), we define \({\bf A}^s = {\bf W \Lambda}^s {\bf W}^{-1}\) where \[\Lambda^s = \begin{bmatrix} \lambda_1^s & 0 & 0 \\ 0 & \ddots & 0 \\0&0&\lambda_n^s\end{bmatrix}.\]

2.4.7 Hadamard (elementwise) operations

Given two matrices \({\bf A},\,{\bf B}\in\mathbb{R}^{m\times n}\) with the same number of rows and columns, we define Hadamard product and division as \[\begin{align*} {\bf A} \odot {\bf B} \in \mathbb{R}^{m\times n} & \text{ such that } ({\bf A}\odot {\bf B})_{ij} = {\bf A}_{ij}{\bf B}_{ij} \\ {\bf A} \oslash {\bf B} \in \mathbb{R}^{m\times n} & \text{ such that } ({\bf A}\oslash {\bf B})_{ij} = \frac{{\bf A}_{ij}}{{\bf B}_{ij}} \end{align*}\] Unlike standard matrix multiplication, the Hadamard product \(\odot\) is commutative such that \({\bf B}\odot {\bf A} = {\bf A}\odot {\bf B}\). Commutativity does not hold for Hadamard division however.

Furthermore, we define Hadamard powers as \[{\bf A}^{\circ k} \in\mathbb{R}^{m\times n} \text{ such that } \left({\bf A}^{\circ k}\right)_{ij} = \left({\bf A}_{ij}\right)^k.\] For the special case \(k=-1\), we refer to \({\bf A}^{\circ (-1)}\) as the Hadamard inverse.

2.5 Exercises

2.5.1 Probability

  1. Given a random vector \(\vec{x}=({\bf x}_1,{\bf x}_2)^T \sim \mathcal{N}(\vec{\mu}, \mathbf{\Sigma})\) where: \[ \vec{\mu} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} , \quad \mathbf{\Sigma} = \begin{pmatrix} 1 & 0 \\ 0 & 10 \end{pmatrix} \]

    1. What are the means and variances of the individual components \(x_1\) and \(x_2\)?

    2. What is the covariance and correlation between \(x_1\) and \(x_2\)?

    3. Are \({\bf x}_1\) and \({\bf x}_2\) independent?

  2. Given a random vector \(\vec{x}=(x_1,x_2)^T \sim \mathcal{N}(\vec{\mu}, \mathbf{\Sigma})\) where: \[ \vec{\mu} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} , \quad \mathbf{\Sigma} = \begin{pmatrix} 4 & 2 \\ 2 & 3 \end{pmatrix} \]

    1. What are the means and variances of the individual components \({\bf x}_1\) and \({\bf x}_2\)?

    2. What is the covariance and correlation between \({\bf x}_1\) and \({\bf x}_2\)?

    3. Are \({\bf x}_1\) and \({\bf x}_2\) independent?

  3. Given a random vector \(\vec{x} = (x_1,x_2) \sim t_{10}(\vec{\mu},{\bf \Sigma})\) where: \[\vec{\mu} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} , \quad \mathbf{\Sigma} = \begin{pmatrix} 1 & 0 \\ 0 & 10 \end{pmatrix}\]

    1. What are the means and variances of the individual components \({\bf x}_1\) and \({\bf x}_2\)?

    2. What is the covariance and correlation between \({\bf x}_1\) and \({\bf x}_2\)?

    3. Are \({\bf x}_1\) and \({\bf x}_2\) independent?

  4. Given a random vector \(\vec{x} = (x_1,x_2) \sim t_{10}(\vec{\mu},{\bf \Sigma})\) where: \[\vec{\mu} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} , \quad \mathbf{\Sigma} = \begin{pmatrix} 4 & 2 \\ 2 & 3 \end{pmatrix}\]

    1. What are the means and variances of the individual components \({\bf x}_1\) and \({\bf x}_2\)?

    2. What is the covariance and correlation between \({\bf x}_1\) and \({\bf x}_2\)?

    3. Are \({\bf x}_1\) and \({\bf x}_2\) independent?

2.5.2 Calculus

  1. Let \(f(\vec{x}) = \vec{x}^T {\bf A}\vec{x}\) for a vector \(\vec{x}\in \mathbb{R}^d\) and a matrix \({\bf A}\in\mathbb{R}^{d\times d}\) which is constant. Give expressions for \(\nabla f\) and \(\mathcal{H} f\) using only matrices and vectors (no summation notation is allowed).

  2. Let \(\vec{x}\in\mathbb{R}^m\) and \(\vec{y}\in\mathbb{R}^n\). Compute the gradient of \(\|\vec{x}\vec{y}^T\|_F^2\) with respect to \(\vec{x}\).

  3. Consider the function \[f(x_1,x_2,x_3) = 2x_1^2 + 3x_2^2 +4x_3^2 + 5x_1x_2+6x_1x_3+7x_2x_3 + 8x_1+9x_2+10x_3 + 11\]

    1. Find the critical point(s) of \(f\). Hint: it may be helpful to express \(f\) in the form \(f(\vec{x})=\vec{x}^T{\bf A}\vec{x} + \vec{b}^T\vec{x} + c\) for some matrix \({\bf A}\), vectors \(\vec{b},\vec{x}=(x_1,x_2,x_3)^T\in\mathbb{R}^3\) and scalar \(c\).

    2. Classify the critical point(s) found in part (a) as minima, maxima, or saddle points. Explain your reasoning.

  4. Verify that the mean and variance of the \(\mathcal{N}(\vec{\mu},{\bf \Sigma})\) distribution are indeed \(\vec{\mu},\,{\bf \Sigma}\) respectively by computing the integrals directly.

  5. Verify that the mean and variance of the \(t_\nu(\vec{\mu},{\bf \Sigma}\) distribution by computing the integrals directly. You may assume that \(\nu > 2.\)

2.5.3 Linear Algebra

  1. Given a matrix \(\mathbf{A} \in \mathbb{R}^{3 \times 3}\) and a vector \(\mathbf{x} \in \mathbb{R}^{3}\), where: \[ \mathbf{A} = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} , \quad \mathbf{x} = \begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix} \]

    1. Compute the product \(\mathbf{A}\mathbf{x}\) using the column interpretation of matrix-vector multiplication.

    2. Compute the product \(\mathbf{A}\mathbf{x}\) using the row interpretation of matrix-vector multiplication.

  2. Given matrices \(\mathbf{A} \in \mathbb{R}^{2 \times 3}\) and \(\mathbf{B} \in \mathbb{R}^{3 \times 2}\), where: \[ \mathbf{A} = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{pmatrix} , \quad \mathbf{B} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} \]

    1. Compute the product \(\mathbf{C} = \mathbf{A}\mathbf{B}\) using the dot product interpretation of matrix-matrix multiplication.

    2. Compute the product \(\mathbf{C} = \mathbf{A}\mathbf{B}\) using the column interpretation of matrix-matrix multiplication.

    3. Compute the product \(\mathbf{C} = \mathbf{A}\mathbf{B}\) using the row interpretation of matrix-matrix multiplication.

  3. Let \({\bf A}\in \mathbb{R}^{m\times n}\).

    1. Explain why \({\bf A A}^T\) and \({\bf A}^T{\bf A}\) are diagonalizable and positive semi-definite.

    2. Give expressions for the singular vectors and singular values of \({\bf A}\) in terms of the eigenvectors and eigenvalues of \({\bf A A}^T\) and \({\bf A}^T{\bf A}\).

  4. Let \[{\bf A}= \begin{bmatrix} 1 & 2 &3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}\]

    1. Show that \({\bf A}^2 \ne {\bf A}^{\circ 2}\).

    2. Under what conditions does \({\bf A}^k = {\bf A}^{\circ k}\) for a square matrix \({\bf A}\)?

2.5.4 Hybrid Problems

  1. Consider the data matrix \[{\bf X} = \begin{bmatrix} 2 & 3 \\ 4 & 5\\ 6& 7 \\ 8 & 9 \end{bmatrix}.\]

    1. Compute the sample mean of the data.
    2. Provide the centered data matrix.
    3. Compute the sample covariance matrix of \({\bf X}.\)

  2. Consider a random vector \(\mathbf{X} \sim \mathcal{N}(\mathbf{\mu}, \mathbf{\Sigma})\) where: \[\mathbf{\mu} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} , \quad \mathbf{\Sigma} = \begin{pmatrix} 1 & 0.5 \\ 0.5 & 1 \end{pmatrix}.\] Let \(\mathbf{Y} = \mathbf{A}\mathbf{X} + \mathbf{b}\) where: \[ \mathbf{A} = \begin{pmatrix} 2 & 1 \\ 1 & 3 \end{pmatrix} , \quad \mathbf{b} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} \]

    1. What is the mean vector \(\mathbf{\mu_Y}\) of \(\mathbf{Y}\)?

    2. What is the covariance matrix \(\mathbf{\Sigma_Y}\) of \(\mathbf{Y}\)?

  3. Given a random vector \(\vec{x}\) with mean \(\vec{\mu}\) and covariance matrix \({\bf \Sigma} = E[(\vec{x}-\vec{\mu})(\vec{x}-\vec{\mu})^T\,]\) verify the identity \({\bf \Sigma} = E[\,\vec{x}\,\vec{x}^T\,] - \vec{\mu} \,\vec{\mu}^T\).

  4. Suppose \(\vec{x}\in \mathbb{R}^n\) is a random vector with covariance \({\bf \Sigma}\in\mathbb{R}^{n\times n}\), and let \({\bf A} \in \mathbb{R}^{m\times n}\) be a matrix with constant entries (non-random). Show that the covariance matrix of \({\bf A}\vec{x}\) is \({\bf A\Sigma A}^T.\)

  5. Show that the \(N\times N\) centering matrix \({\bf H} = {\bf I} - \frac{1}{N}\mathbb{1}\mathbb{1}^T\) is idempotent, i.e. \({\bf H}^2 = {\bf H}.\)

  6. Consider the data matrix \[{\bf X}=\begin{bmatrix}\vec{x}_1^T \\ \vdots \\ \vec{x}_N^T\end{bmatrix}.\] Show that \[{\bf HX} = \begin{bmatrix} \vec{x}_1^T -\bar{x}^T \\ \vdots \\ \vec{x}_N^T - \bar{x}^T\end{bmatrix}\] where \({\bf H}\) is the centering matrix and \(\bar{x}\) is the sample mean of vectors \(\vec{x}_1,\dots, \vec{x}_N.\)

  7. For data \(\vec{x}_1,\dots,\vec{x}_N\) with sample mean \[\hat{\mu}= \frac{1}{N}\sum_{i=1}^N \vec{x}_i\] and sample covariance \[\hat{\bf \Sigma} = \frac{1}{N} (\vec{x}_i-\hat{\mu})(\vec{x}_i-\hat{\mu})^T\] verify the following identities

    1. \(\hat{\bf \Sigma} = \frac{1}{N}\left(\sum_{i=1}^N \vec{x}_i\vec{x}_i^T\right) - \hat{\mu}\hat{\mu}^T.\)

    2. \(\hat{\bf \Sigma} = {\bf X}^T {\bf H X}\) where \({\bf X}\) is the data matrix formed from vectors \(\vec{x}_1,\dots,\vec{x}_N\).

References

[4]
Trefethen, L. N. and Bau, D. (1997). Numerical linear algebra. SIAM.
[5]
Strang, G. (2006). Linear algebra and its applications. Thomson, Brooks/Cole, Belmont, CA.